Aproksymacja wykresów liniowych

Zgodnie z definicją, aproksymacja to proces poszukiwania rozwiązania przybliżonego, gdzie funkcję (byt) dokładną zastępuje się funkcją prostszą (np. wielomianem niższego rzędu).

W odróżnieniu od interpolacji, funkcja aproksymująca nie wymaga, aby wykres jej przechodził przez znane i zadane punkty. Przy poszukiwaniu rozwiązania zadania aproksymacji zwykle wyznacznikiem jest znalezienie takiej funkcji, dla której błąd aproksymacji (np. średni błąd kwadratowy) nie przekracza wartości zadanej. W tym artykule spojrzymy szerzej na sposoby aproksymacji danych obrazujących wartości wielkości fizycznych.

Podejście do aproksymacji funkcji zwykle różni się w zależności od tego, czy dane poddane aproksymacji są szybkozmienne, czy wolnozmienne.

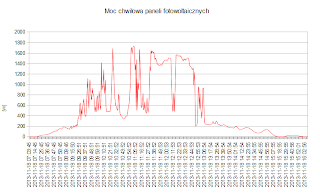
Poniższy wykres przedstawia moc chwilową paneli fotowoltaicznych zanotowaną w dniu 18 listopada 2013 r. Punkt pomiarowy trwa 1 minutę. Na podanym wykresie jest ujęta tylko część dnia, podczas której panele fotowoltaiczne pracują, czyli oddają moc. Poniższy wykres składa się z 490 punktów pomiarowych (czyli okres na nim przedstawiony wynosi 490 minut).

Skomentujmy ten wykres. Należy zauważyć, że punkt pomiarowy trwa 1 min, a wielkość mierzona silnie zależy na natężenia oświetlenia. Często w ciągu dnia zdarzają się przygaśnięcia słońca czy przysłonięcia przez chmury, dlatego wykres ten należy potraktować jak dane szybkozmienne. Widać jak bardzo poszarpany jest ten wykres. Po drugie powyższy wykres został wykreślony z użyciem 490 punktów pomiarowych. To zdecydowanie za dużo oraz niepotrzebnie, aby oko ludzkie oceniło zmiany mocy paneli fotowoltaicznych w ciągu dnia. Można rzec, że bez uszczerbku dla zrozumienia wykresu można by wykreślić powyższy wykres z użyciem ilości punktów pomiarowych 10 razy mniejszej. To oczywiście kwestia podstawowa, co chcemy odczytywać z wykresu i jak to interpretować. Jednak jeśli powyższy wykres ma służyć jedynie człowiekowi aby wizualnie oceniał moc paneli fotowoltaicznych w poszczególnym dniu, to taka duża ilość danych jest niepotrzebna.

Powyższy wykres został wykreślony z użyciem co 10-ego punktu pomiarowego. Wykres jest bardziej gładki, jednak można zauważyć jedną rzecz. W czasie dnia słońce przygasało i zaświecało się dość często i w przypadku gdy do kreślenia bierzemy co 10-ty punkt pomiarowy, te chwilowe zmiany mocy paneli fotowoltaicznych są słabo widoczne. Po prostu kreśliliśmy linię od punktu 10 do punktu 20, od punktu 20 do punktu 30, od punktu 30 do punktu 40 itd. Wszystko pomiędzy (np. punkt nr 11, 12, 15, 23, 34) jest tracone i nie zostało pokazane na wykresie. W przypadku graficznej aproksymacji wykresu ważne może być nie tylko oddanie wiarygodnej wartości przebiegu czasowego, ale także prawidłowe obliczenia całki czy różniczki krzywej. W podanym tu przypadku całka z wykresu oddaje uzysk energetyczny paneli fotowoltaicznych w ciągu całego dnia, czyli ile kWh energii panele fotowoltaiczne wyprodukowały w ciągu dnia.

Prostym zabiegiem mogącym poprawić oddawanie rzeczywistego stanu na wykresach jest kreślenie wykresu na podstawie średniej arytmetycznej z kilku punktów pomiarowych. Dla naszego przykładu mocy paneli fotowoltaicznych, narysujmy wykres składający się z 10 razy mniejszej ilości danych niż oryginalny wykres z surowych danych, ale z uśrednionymi punktami pomiarowymi.

Na pierwszy rzut oka widać jedną rzecz. Na oryginalnym wykresie około godz. 12:11 zaszło słońce i moc paneli fotowoltaicznych spadła. Na drugim naszym wykresie (co 10-ty punkt pomiarowy) nie widać tego momentu, gdyż akurat pominęliśmy te punkty pomiarowe. Lepszym rozwiązaniem jest trzecie, który uwzględnia średnią z 10-ciu punktów pomiarowych i na tej podstawie kreśli wykres.

Podsumowanie

Najlepszym podsumowaniem jest nałożenie na siebie wszystkich trzech wykresów.

Kolorem czerwonym oznaczono surowe dane, czyli rzeczywiste wartości. Linia fioletowa obrazuje dane z co 10-go punktu pomiarowego, a linia niebieska obrazuje uśrednione dane z 10 punktów pomiarowych.  Można zauważyć, że fioletowa linia przebiega dokładnie w tych samych punktach, co wykres czerwony. Nie ma to miejsca na wykresie niebieskim, gdzie wartość danego punktu zależy od średniej 10 wcześniejszych punktów pomiarowych. Wykres niebieski lepiej oddaje dynamikę (zmienność) funkcji, podczas gdy wykres fioletowy prowadzi punkty dokładnie w miejscach rzeczywistego ich występowania. Jednak ze względu na 10-krotnie mniejszą liczbę danych pomiarowych, nie ma sensu kreślić wykresu dokładnie w wartościach rzeczywistych pomiarów (linia fioletowa), ale lepiej policzyć średnią (linia niebieska) i narysować punkt tam, gdzie wskazuje średnia z x pomiarów. Linia niebieska lepiej oddaje też zmienność rzeczywistych danych i zapobiega "przeskoczeniu" punktu pomiarowego poza dziurę lub pik, gdyż wtedy średnia punktu pomiarowego będzie odpowiednio mniejsza lub większa. Natomiast taki wykres z 49 punktami pomiarowymi błyskawicznie może być wyrysowany przez skrypt i zrenderowany w programie użytkownika. Większa ilość punktów pomiarowych na wykresie wiąże się z tym, że jest on dłużej renderowany.

Wspomniałem, że czasami trzeba trzeba iść na kompromis i tak namalować wykres, aby dobrze oddawał on dynamikę badanego przebiegu, a jednocześnie z małym błędem obliczał pole pod krzywą (całkę).

Całka z rzeczywistych danych pomiarowych (490 punktów, czerwony wykres) wyniosła 4,034 kWh. To przyjmijmy za punkt odniesienia. Metoda rysowania wykresu co 10-ty punkt pomiarowy dała wynik uzysku energetycznego 4,097 kWh (+1,56 %). Metoda uśredniania 10-ciu punktów pomiarowych dała wynik 4,034 kWh. Akurat przypadek sprawił, że pokrywa się to dokładnie z wartością rzeczywistą, ale z całą pewnością wynik całki przy wykorzystaniu tej metody powinien być bardziej dokładny.